Les opérateurs booléens
Problème posé :
On vous propose de concevoir un additionneur binaire à partir d'opérateurs booléens. On vous rappelle le principe de l'addition binaire ci-dessous:
Soit l'addition entre deux données a et b de taille 1 bit, on appelle S la somme et R la retenue éventuelle, l'addition s'écrit:
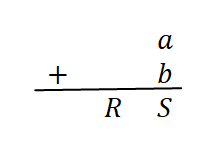
Si a = 0 et b = 0 => S = a+b => S = 0+0 = 0 => la somme S=0 et la retenue R=0:
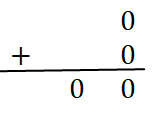
Si a = 0 et b = 1 => S = a+b => S= 0+1 = 1 => la somme S=1 et la retenue R=0
Si a = 1 et b = 0 => S = a+b => S= 1+0 = 1 => la somme S=1 et la retenue R=0:
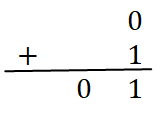
Si a = 1 et b = 1 => S = a+b => S = 1+1 => la somme S=0 La retenue R=1
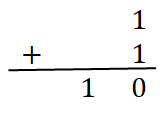
Travail demandé:
1. Compléter la table de vérité de l'addition entre les deux données a et b de taille 1 bit, on appelle S la somme et R la retenue:

2. Exprimer l'équation de la somme S en fonction de a et b et l'équation de R en fonction de a et b.
3. Télécharger le logiciel logisim en cliquant ici
Renommer l'extension logisim.job devient logisim.jar pour rendre le programme java exécutable
Regarder la vidéo d'utilisation de logisim en cliquant ici
Dessiner avec le logiciel "Logisim" le logigramme de l'additionneur à partir des équations obtenues à la question précédente.
4. On vous donne le montage suivant réalisé avec Logisim:
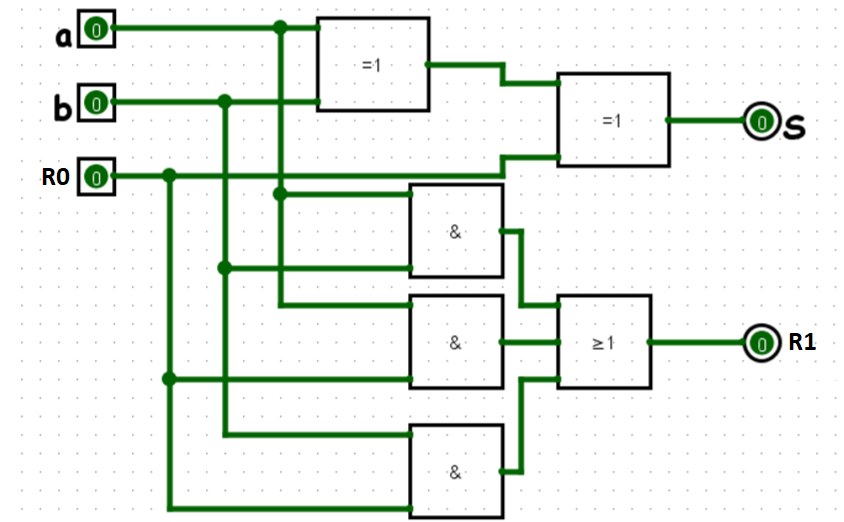
4.1 Dessiner ce montage avec logisim et établir la table de vérité des sorties S et R1 en fonction de a, b et R0 dans le cas particulier où R0=0. Montrer que le montage se comporte comme un additionneur de somme S et de retenue R1.
5. Si on considère que R0 est une retenue initiale, l'état R0=0 est logique car il n'y a pas de raison d'avoir une retenue initiale, le calcul peut se décrire ainsi:
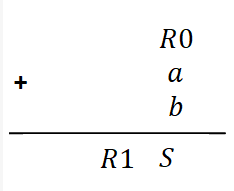
On veut construire, en utilisant plusieurs additionneurs de données 1 bit, un additionneur de deux données de 4 bits a=a3a2a1a0 et b=b3b2b1b0 dont l'addition se décrit ainsi:

5.1 On considère deux données de 4 bits: a=1010 et b=1101, préciser la valeur de a0,a1,a2,a3 et b0,b1,b2,b3 dans ce cas.
5.2 Effectuer l'addition des deux données précédentes si R0=0, préciser la valeur de R4, S3, S2, S1 et S0 dans ce cas
5.3 Concevoir l'additionneur avec logisim et vérifier votre résultat de la question précédente.
Créé avec HelpNDoc Personal Edition: Documentation Qt Help facile