Algorithme k plus proches voisins

Algorithme des k plus proches voisins ou "knn"

Partie A : travaux préliminaires

Question A1

On considère une liste de tuples qui représentent des points dans un espace affine à deux dimensions:

la_liste_de_tuples = [('A', 47, 100), ('B', 77, 79), ('C',74, 31)]

Ecrire le code d'une boucle for avec itérateur pour afficher chaque tuple.

Ecrire le code d'une boucle for avec plage range pour afficher chaque tuple.

Dans les deux cas  le rendu sera:

Question A2

Ecrire une fonction affiche qui prend en paramètre une liste de tuples à trois éléments comme la_liste_de_tuples et qui permet d'afficher le détail de chacun des tuples; pour la liste analysée, l'appel  affiche(la_liste_de_tuples)  donnera:

Pour la liste L = [('F', 19, 78), ('G', 81, 7), ('H', 85, 1), ('I', 6, 33),('J',22, 26)], l'appel  affiche(L)  donnerait:

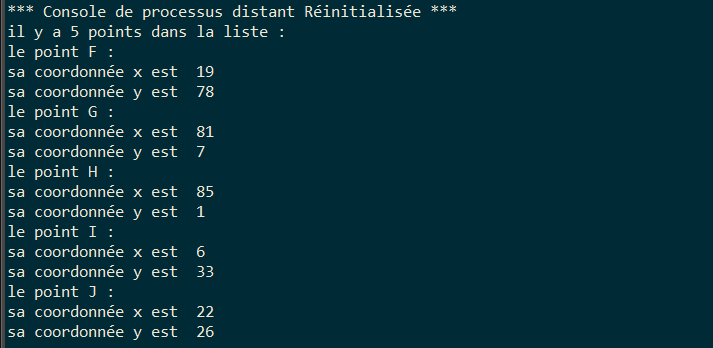
Partie B : le plus proche voisin

On considère maintenant un ensemble de points répartis dans un plan X, Y.

Un repère orthonormé nous permet de définir les coordonnées de ces points:

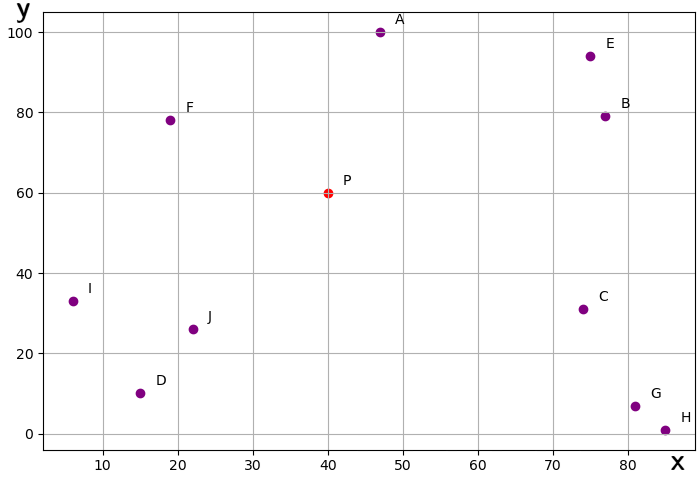
On stocke tous les points dans un tableau qui utilise un tuple pour chaque point comme dans la partie A.

 Par exemple le point A (47,100) devient dans le tableau le tuple :

('A', 47, 100) 

Le tableau  la_liste_des_points est une liste de tuples:

la_liste_des_points = [('A', 47, 100), ('B', 77, 79), ('C',74, 31),( 'D', 15, 10), ('E', 75, 94), ('F', 19, 78), ('G', 81, 7), ('H', 85, 1), ('I', 6, 33),('J',22, 26)]

Le repérage des éléments de la liste nécessite 2 indices: l'indice dans la liste et l'indice dans le tuple:

Pour accéder aux valeurs du point A en python:  

nom_point  =  la_liste_des_points [0] [0]    <=> nom_point = 'A'

coordonnée_XA = la_liste_des_points [0] [1]    <=> coordonnée_XA = 47

coordonnée_YA = la_liste_des_points [0] [2]    <=> coordonnée_YA = 100

Le point P en rouge sur le graphe est celui dont on va chercher les plus proches voisins.

Il aura sur le modèle précédent de liste de points les coordonnées :   pointP = [('P', 40, 60)]

Sa coordonnée_Xp= 40 et sa coordonnée_Yp = 60;  en python: pointP[0][1] = 40  et pointP[0][1] = 60

Question B1

En vous aidant du cours calculer la distance entre le point P et le point A.  Écrire votre calcul dans le compte rendu.

Écrire le code python qui ferait calcul dans votre compte rendu.

Question B2

On vous donne la liste de tous les points et un code qui permet de dessiner ces points avec avec Matplotlib

la_liste_des_points = [('A', 47, 100), ('B', 77, 79), ('C',74, 31),( 'D', 15, 10), ('E', 75, 94), ('F', 19, 78), ('G', 81, 7), ('H', 85, 1), ('I', 6, 33),('J',22, 26)]

# ne pas oublier d'importer  matplotlib

import matplotlib.pyplot as plt

def dessine_points(la_liste_des_points,color):

    a,x,y = zip(*la_liste_des_points)

    plt.scatter(x, y, c=color)

    for a in la_liste_des_points: plt.annotate(a[0], (a[1]+2, a[2]+2))

# Utilisation des fonctions (à la fin du code) :

pointP=[('P', 40, 60)]

dessine_points(la_liste_des_points,'green')

dessine_points(pointP,'purple')

plt.xlabel('exemple', fontsize=14)

plt.grid()

plt.show()

Utiliser ce code et Mettre une capture d'écran en mettant

  - les points de la liste en mauve et le point P en rouge

  - les titres des 2 axes

dans votre compte rendu.

Question B3

Écrire une fonction appelée distance( point1, point2 ) qui calcule la distance euclidienne entre deux points passés en paramètres ( utiliser le co./fichiers/cours_knn.pdfurs et voir INFOS ci dessous)

Par exemple  distance ( (47,100) , (40, 60)  ) calculera la distance entre le point A et le point P.

Question B4

On donne ci-dessous une fonction appelée  calcule_la_distance (Une_liste_de_points, Un_point) qui permet de calculer la distance d'un point P par rapport à tous les points d'une liste.

Cette fonction prend deux paramètres: "la liste des points" à considérer et "un point" comme  les coordonnées du point P étudié.

Durant son exécution, elle construit une  liste de tuples points/distances qui contient pour chaque point de la liste,  le nom du point en chaîne de caractères et la distance qui le sépare du point P comme valeur, la fonction affiche la liste en fin d'exécution.

Utilisation

def calcule_la_distance (Une_liste_de_points, Un_point):

    #la liste de tuples point/distances
    lstuplepointdistances = []
    for i in range (len(Une_liste_de_points)):

        # à remplacer suite à la question:
        distance_par_rapport_à_P =  distance ( (47,100) , (40, 60)  )

        # Ajout à la liste de tuples point/distances,

        # on aurait pu utiliser lstuplepointdistances.append(...) pour l'ajout.
        lstuplepointdistances = lstuplepointdistances + [(Une_liste_de_points[i][0],distance_par_rapport_à_P)]
    print("Les distances de chaque point : ", lstuplepointdistances)

Modifier cette fonction pour qu'elle utilise les paramètres Une_liste_de_points et Un_point avec votre fonction distance( point1, point2)  pour calculer la distance, Tester votre code.

On utilise la fonction en passant la liste La_liste_des_points et le point P:

La_liste_des_points= [('a', 47, 100), ('b', 77, 79), ('c', 74, 31), ('d', 15, 10), ('e', 75, 94), ('f', 19, 78), ('g', 81, 7), ('h', 85, 1), ('i', 6, 33), ('j', 22, 26)]

pointP = ('P', 40, 60)

calcule_la_distance (La_liste_des_points, pointP):

Elle affichera:

Question B5

Relire les notions sur le tri des tuples et  classer  lstuplepointdistance suivant la distance des points les plus proches de P (ordre croissant)

Question B6

On veut pouvoir afficher la distance d'un nombre k quelconque de voisins proches.

- Ajouter un paramètre "nombres_de_voisins" à la fonction calcule_la_distance (Une_liste_de_points, Un_point, nombres_de_voisins):

# calcule et affiche les distances de 3 voisins
calcule_la_distance(la_liste_des_points, P, 3)

Partie C : La classe d'appartenance

Question C1

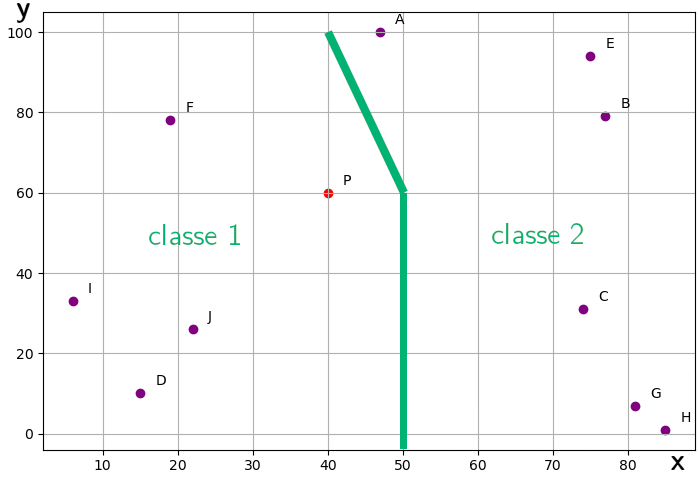
Tous les points qui sont à gauche du trait vert ci-dessous appartiennent à la classe 1, tout ceux à droite de ce trait appartiennent à la classe 2.

Copier puis compléter une nouvelle liste de tuples des points de départ (rappelée ci-dessous), pour ajouter la classe d'appartenance des points:

 la_liste_des_points = [('A', 47, 100), ('B', 77, 79), ('C',74, 31),( 'D', 15, 10), ('E', 75, 94), ('F', 19, 78), ('G', 81, 7), ('H', 85, 1), ('I', 6, 33),('J',22, 26)]

 la_liste_des_points_classe = [('A', 47, 100, " classe2"), ...

Question C2

Modifier la fonction calcule_la_distance() pour qu'en s'appuyant sur le nombre k de voisins proches, elle  puisse déterminer à quelle classe appartient le point P. Vérifier comment se comporte votre code pour k = 1 voisin, k = 3 voisins et k = 5 voisins.

Créé avec HelpNDoc Personal Edition: Produire des livres Kindle gratuitement