Flash-codes: les DataMatrix
Problème posé :
Un DataMatrix est une petite image en noir et blanc qui contient une information codée. Le principe est d'utiliser des informations numériques qui sont représentées en deux dimensions. Un appareil tel qu'un smartphone peut décoder l'information avec une application dédiée comme l'application gratuite "Flashcode" par exemple. Les DataMatrix font l’objet de plusieurs normes dont la norme ISO/IEC 16022. Ils permettent de coder les caractères alphanumériques ( les lettres et les chiffres); vous pouvez, par exemple, coder une carte de visite avec un dataMatrix. Voici l'apparence d'un dataMatrix:

Depuis janvier 2011, tous les médicaments vendus en France comportent sur leur emballage un DataMatrix permettant de tracer la provenance, la date de péremption et le nom du médicament.

Un DataMatrix est composé d’une marge pour que le lecteur puisse se repérer, et d’une matrice ( un tableau à 2 dimensions) permettant d’y insérer les données sous forme de code :
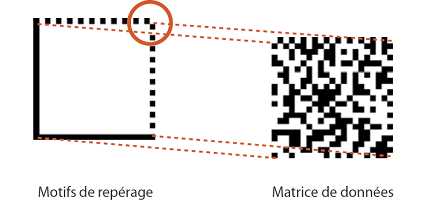
La taille de la matrice dépend du nombre d’informations que l’on souhaite coder. La capacité peut aller jusqu'à 2335 caractères alphanumériques codés dans la matrice.
1.1 Flasher le DataMatrix ci-dessous avec votre smartphone ou une tablette. Indiquer l'information contenue dans le DataMatrix sur votre compte rendu.

Principe du codage d'un dataMatrix
La matrice d’un DataMatrix comporte des nombres binaires appelés "CodeWords" ( mots codés en Anglais). Chaque CodeWord correspond à un octet ( une information sur 8 bits ).
Les CodeWords sont placés dans la matrice binaire selon un procédé décrit par la norme ISO/IEC 16022.
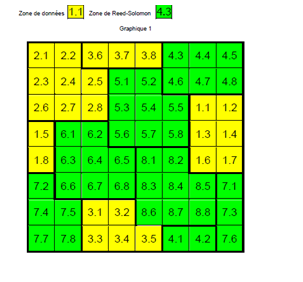
Voici comment sont disposés les CodeWords dans une matrice 8*8 bits:

Comment lire la matrice:
Analysons un nombre binaire de 8 bits: 1010 0100, ce nombre binaire possède son MSB=1 ( le bit de poids fort=1) et son LSB=0 ( son bit de poids faible = 0). Si on veut associer ce nombre à un "CodeWord", on place chaque bit à son emplacement pour le CodeWord choisi. Pour le CodeWord numéro 2 ( celui entouré ci-dessus), les emplacements sont repérés: 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7 et 2.8. Le bit de poids fort doit être placé en "2.1" et le bit de poids faible en "2.8", l'affectation du nombre binaire précédent sera donc 2.1=1, 2.2=0, 2.3=1, 2.4=0, 2.5=0, 2.6=1, 2.7=0 et 2.8=0.
Dans le DataMatrix, on n'écrit pas les 1 et les 0, on utilise la couleur noire pour un bit = 1 et la couleur blanche pour un bit =0, voici le résultat (entouré en rouge ci-dessous) pour l'octet précédent placé dans le codeword2

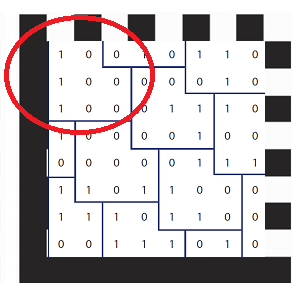

1.2 Combien de CodeWords sont présents dans le DataMatrix ci-dessus ( DataMatrix de matrice 8*8 bits )?
1.3 Donner la valeur numérique des 3 premiers CodeWords du DataMatrix ci-dessus. Les trois premiers CodeWords son repérés de 1.1 à 1.8 pour le premier, de 2.1 à 2.8 pour le second et 3.1 à 3.8 pour le troisième.
1.4 Convertir la valeur de ces 3 CodeWords en base 10 ( expliquer votre méthode)
1.5 Calculer la vraie valeur de chaque CodeWords en retranchant 130 à chaque nombre trouvé à la question 1.4 ( par exemple si le CodeWord1 vaut 142, sa vraie valeur est 12, ce qui veut dire que l'on a codé le chiffre 1 et le chiffre 2 dans le CodeWord)
1.6 Écrire bout à bout la suite des chiffres encodés dans les CodeWord. L'association des chiffres donne-t-elle une suite de chiffres cohérente?
1.7 Flasher le DataMatrix ci-dessous et comparer avec votre décodage:

1.8 Télécharger en cliquant ici le fichier datamatrix carré de 8x8 bits nommé "DataMatrix.xls" (fichier Excel) , on veut coder la série de chiffres « 987654 ».
Le CodeWord1 devra contenir "98" soit 9 et 8 , le CodeWord2 contiendra "76" et le CodeWord3 contiendra "54". Coder chaque Codeword dans le fichier Excel ( n'oubliez pas d'ajouter 130 avant de transcoder le codeword en base 2 ), les CodeWord 4, 5, 6 7, 8 seront ignorés ( bits à 0) pour l'instant. Copier-coller le DataMatrix obtenu sur votre compte rendu.
ATTENTION: si vous flashez votre DataMatrix après remplissage des 3 CodeWords, vous n'obtiendrez rien parce que la matrice dit aussi contenir la valeur des codewords 4, 5, 6, 7, 8 qui contiennent un code de vérification d'erreur.
Code de Vérification d'erreur
Sur les 8 CodeWords d'une matrice "8x8" , les CodeWords 4,5,6,7,8, sont réservés à la vérification de l’information pour éviter les erreurs de lecture. La vérification est basée sur l’algorithme de REED-SOLOMON qui met en œuvre des concepts mathématiques complexes. Vous disposez du programme "Reed-Solomon.exe" qui va vous fournir les cinq octets de vérification pour les DataMatrix de 8x8 bits.
1.9 Télécharger en cliquant ici l’exécutable "Reed-Solomon.exe" joint à cette activité pour connaître la valeur des 5 octets de vérification associés aux trois CodeWords 228 ; 206 ; 184.
1.10 Compléter le datamatrix en ajoutant la valeur binaire des 5 octets de vérification d'erreur obtenus précédemment dans le fichier Excel "DataMatrix.xls".
Attention: ne pas ajouter 130 aux valeurs des 5 octets de vérification.
Copier-coller votre DataMatrix sur votre compte rendu.
1.11 Flasher le DataMatrix pour vérifier que l’information fournie est correcte.
1.12 Sur Excel DataMatrix.xls, changer deux bits du DataMatrix. Flasher le DataMatrix, vérifier l’information fournie. Changer deux autres bits du DataMatrix, Flasher le DataMatrix, vérifier à nouveau l’information fournie. Au bout de combien de bits changés, le système ne peut plus lire le DataMatrix?
Créé avec HelpNDoc Personal Edition: Documentation Qt Help facile