Algorithmes de programmation dynamique
Partie 2: programmation dynamique
La programmation dynamique est un concept algorithmique qui se base sur la décomposition d’un problème difficile en sous problèmes plus simples. Le principe utilisé ici s’appelle la mémoïsation, c’est à dire la mémorisation des valeurs intermédiaires des sous problèmes dans un cache pour éviter que ces données ne soient calculées plusieurs fois.
Tous les problèmes ne peuvent pas utiliser cette méthode, il faut que le problème possède deux caractéristiques :
- Une sous structure optimale : un problème a une sous structure optimale s’il peut se décomposer en sous problèmes et si la solution optimale peut se calculer à partir de la solution optimale de ses sous problèmes. Un tel problème peut se modéliser avec un graphe.
- des sous problèmes superposés : un problème avec sous problèmes superposés nécessite de calculer plusieurs fois le(s) même(s) sous-problème(s)
Question 2.1
On considère les 8 premiers termes de la une suite de Fibonnacci: 1 1 2 3 5 8 13 21
- les deux premières valeurs sont égales à 1 ( cas de base );
- ensuite, chaque valeur est obtenue en faisant la somme des deux valeurs qui la précèdent ( cas récursif ).
La troisième valeur est donc 1+1 = 2 , la quatrième est 1 + 2 = 3 , la cinquième est 2+3 = 5 et ainsi de suite.
Ecrire la fonction fibo(n) qui calcule récursivement et renvoie la valeur du terme n de la suite, fibo(0) renvoie 1, fibo(1) renvoie 1, fibo(2) renvoie 2, fibo(4) renvoie 5
Question 2.2
On vous donne ci-dessous le graphe des appels récursifs pour fibo(4):
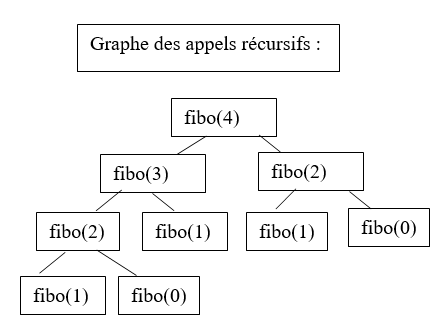
On peut constater que fibo(2) est calculé 2 fois, fibo(1) est calculé 3 fois et fibo(0) est calculé 2 fois.
Etablir le graphe de fibo(5) , lister tous les calculs redondants qu'effectue l'algorithme récursif pour déterminer ce terme.
La programmation dynamique va permettre d’organiser le calcul de manière à ne pas recalculer ce qui l’a déjà été
Le graphe ci-dessous montre ce que l'on va faire pour fibo(4) à savoir ne pas recalculer plusieurs fois les valeurs fibo(2) , fibo(1) et fibo(0)
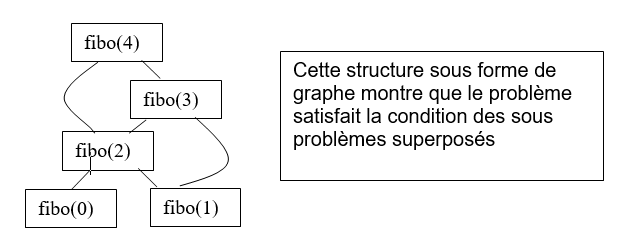
On peut partir de fibo(0) et fibo(1) qui sont connus et remonter le graphe en mémorisant les valeurs calculées, c'est la méthode ascendante dite bottom-to-up
On peut partir de fibo(n) et descendre récursivement le graphe en mémorisant les valeurs calculées, c'est la méthode descendante dite up-to-bottom
Question 2.3: méthode ascendante
- Créer la définition de la fonction fibo_ascendant(n) en respectant la méthode suivante:
- la fonction prend en argument le terme n recherché
Dans la fonction: - On crée un liste vide appelée termes
- On ajoute dans la liste termes la valeur de fibo(0) soit 1
- On ajoute dans la liste termes la valeur de fibo(1) soit 1
- On crée une boucle for de i = 2 à i = n, dans cette boucle:
- On ajoute dans la liste termes, la valeur de termes [i-1] + termes[i+2]
- la fonction renvoie la valeur de termes[n]
- Tester la fonction pour fibo_ascendant(4)
Question 2.4: méthode descendante
- Créer la définition de la fonction recursive fibo_descendant(n, termes=None) en respectant la méthode suivante:
- La fonction prend en arguments n le terme recherché et une variable termes initialement égale à l'objet None ( cette variable va devenir la liste des termes de la suite)
Dans la fonction: - Si la variable termes est l'objet None ( ce qui est le cas au début) , on lui associe une liste comprenant n+1 fois l'objet None
- Si termes[n] vaut None ( on n'a pas encore calculé la valeur du terme n) alors:
- si n est inférieur ou égal à 1 , on affecte termes[n] = 1 ( pour les deux premiers termes de la suite )
- sinon on calcule recursivement termes[n] = fibo_descendant(n-1,termes) + fibo_descendant(n-2,termes)
- Sinon ( termes[n] ne vaut pas None ) la fonction renvoie la valeur de termes[n]
- Tester la fonction pour fibo_ascendant(4)
Créé avec HelpNDoc Personal Edition: Nouvelles et informations sur les outils de logiciels de création d'aide