Calculabilité

Annexe 1

Décidabilité

Une propriété est décidable si on peut déterminer en un nombre fini d'étapes si elle est vraie ou fausse quel que soit le contexte de départ (on parle de problème de décision, à réponse oui ou non).

Exemple : Est-ce qu’un nombre est pair est une propriété décidable.

Calculabilité

Une fonction f est dite calculable s'il existe un algorithme capable de donner la valeur de f(x) pour tout x.

Un calcul mathématique se réduit à une succession d'opérations élémentaires

• Les nombres calculables sont des nombres qui sont générables en un nombre fini d'opérations élémentaires ( addition, soustration,..) .
• Une fonction mathématique est calculable s'il existe une suite finie d'opérations élémentaires permettant de passer d'un nombre x à son image f(x) »
  
  

En informatique on classe les problèmes à calculer par classe de complexité en temps de calcul.

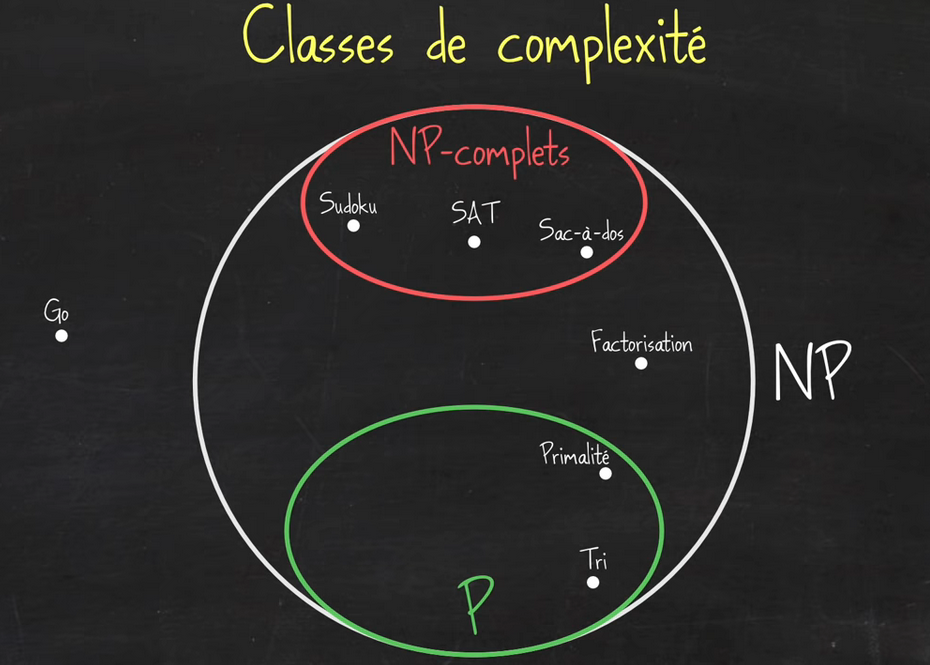
On définit la classe P,  un problème de classe P est un problème que l'on sait résoudre en temps t raisonnable, c’est à dire un problème de complexité linéaire, quadratique ou logaritmique.

Exemples :

- t = f(n) : parcourir une liste  ( le temps d’exécution est fonction du nombre de données n)

- t = f(n2): trier une liste ( le temps d’exécution est fonction du carré du nombre de données n)

- t = f(log2(n)): trouver un nombre par dichotomie ( le temps d’exécution est fonction du logarithme de base 2 du nombre de données n)

- t = f(nxlog(n)): trier une liste par  tri-fusion ( le temps d’exécution est fonction du produit du nombre de données n  par le logarithme de base 2 du nombre de données n)

On définit aussi la classe NP qui  décrit des problèmes qui quand ils sont calculables le sont en un temps polynomial (exponentiel par exemple ) par une machine non déterministe, c’est à dire par une machine capable d'explorer simultanément plusieurs solutions possibles, ce qui n’existe pas vraiment. On peut imaginer un arbre dont le parcours se ferait simultanément dans toutes les branches, et non en largeur ou profondeur comme nous l'avons vu.

Certains problèmes dans NP ont une propriété remarquable :

La résolution polynomiale d'un seul d'entre eux ferait ramener la totalité des problèmes NP dans P. On dit que ces problèmes sont NP-complets.

La machine de turing

Le principe

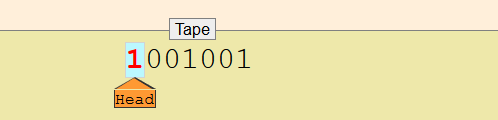
Une machine de Turing est un ruban qui comprend un nombre infini de cases. Une tête de lecture/écriture se déplace de case en case sur le ruban dans les deux sens. Cette tête peut lire le contenu d’une case, l’effacer et le remplacer (écrire) par un autre caractère d’un alphabet reconnu par le logiciel qui gère la machine.

Définition du logiciel 

La machine exécute un programme qui définit un nombre fini d’états E, Parmi les états de E, on distinguera e0, ea et er qui sont respectivement l’état initial (point de départ du programme), l’état d’acceptation (point d’arrêt du programme) et l’état de refus qui est un point d’arrêt atteint en cas d’erreur d’exécution.

La machine manipule des données qui appartiennent à un alphabet de travail T, cet alphabet comprendra tous les caractères reconnus par le programme, T est inclus dans un alphabet fini A qui représenterait tous les caractères que l’on peut saisir au clavier.

De manière plus formelle :

 

- A  est un alphabet fini.

- T ⊃ A est l’alphabet de travail fini de notre machine.
Pour notre logiciel  T = { b, à , e , i , j , l , n , o , p , u , t , r , s , ) , ( , " , ! , § }

On doit aussi inclure le caractère blanc B qui est une case vide sur le ruban.
 

(B peut être utilisé pour créer un espace entre deux caractères)

On définit également une fonction de transition F qui permet de passer d’un état à un autre, elle reçoit en argument l’état où se trouve la machine et le caractère lu par la tête sur le ruban, elle donne comme image un état de la machine, un caractère de l’alphabet de travail à écrire par la tête et la direction à prendre pour la tête de la machine après cette écriture, de manière formelle on peut décrire la fonction de transition ainsi :

F : E × T → E × T × {←,→}

Exemple de logiciel une machine de Turing:

Les lignes de codes représentent les transitions, elles se programment sur une ligne selon la syntaxe générale suivante :

ec  cl ce  d es

Arguments de la fonction : ec (état courant) et  cl (caractère lu à l’emplacement de la tête). 

Image par la fonction : ce (caractère écrit à l’emplacement de la tête en remplacement de cl) ; d (la direction que prendra la tête après l’écriture de ce) et es l’état suivant de la machine :

F(ec,cl) = ce, d, es

Exemple concret:

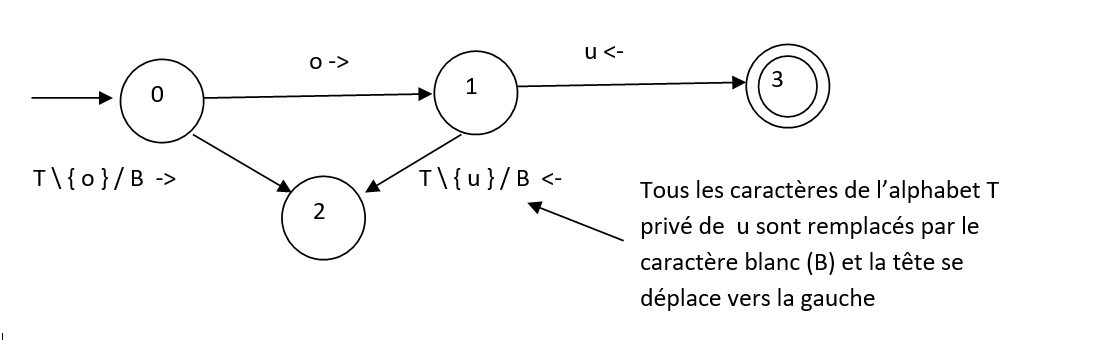
On veut programmer que si la machine est à l’état initial 0 (ec = 0),  si  la tête lit le caractère  o   (cl = o) , elle ne change pas le contenu de la case lue ( ce qui se programme avec le symbole  *, ce=o) , elle déplace la tête à droite ce qui s’écrit r  pour right ( d = r)  et le programme poursuit  à l’état 1 ( es =1) , la programmation de cette transition sera :

0 o * r 1

Toujours à l’état initial 0, si la machine lit n’importe quel autre caractère de l’alphabet T que « o » ce qui se programme avec le symbole * qui représente tous les caractères,  elle le remplace par un blanc (l’effacement se programme avec le symbole  _  ) , elle déplace ensuite la tête à droite (r) et passe à l’état 2, la programmation de cette transition sera :

0 * _ r 2

A l’état 1, si la machine lit le caractère u , elle le laisse dans la case lue ( symbole *), elle déplace la tête à gauche ( symbole l pour left) et passe à l’état 3, la programmation de cette transition sera :

1 u * l 3

Toujours à l’état 1, si la machine lit n’importe quel autre caractère de T que « u » ( symbole  *) ,  elle le remplace par un blanc (symbole _ ) , elle déplace la tête à gauche (l) et passe à l’état 2 , la programmation de cette transition sera :

1 * _ l 2

A l’état 2, quelque soit le caractère lu par la tête (symbole *), il est effacé (symbole _),  la tête ne bouge pas (symbole *), la machine s’arrête c’est l’état de refus :

2 * _ * halt      (autre écriture possible :  2 * _ * halt-reject )  

A l’état 3, quelque soit le caractère de T lu par la tête (symbole *), il n’est pas remplacé (symbole *),  la tête ne bouge pas (symbole *), la machine s’arrête c’est l’état d’acceptation:

3 * * * halt-accept

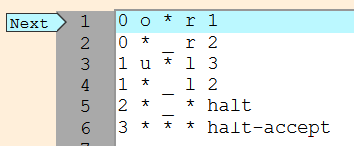
Le programme complet

Test du programme avec votre machine de Turing:

• Connectez vous à l’adresse :  http://morphett.info/turing/turing.html
• Copiez-collez le programme ci-dessus dans la zone de programmation
  
• Saisissez la chaine de caractère « ou » sans les guillemets dans la zone Initial input.  Réinitialisez la tête en cliquant sur Reset :
  
• Testez l’exécution en cliquant sur Step jusqu’à l’arrêt de la machine.
  
  

• Graphe état transition de la machine de Turing

Une machine de Turing  peut se représenter graphiquement par un graphe état-transition dont les sommets sont les états, les arcs représentant les transitions. Le sommet qui représente l’état d’acceptation est marqué par un double cercle.

Une transition  F(e1,cl) = (e2,ce,d), où e1,e2 sont dans E, les caractères cl=c1, ce=c2 dans T et d une direction ( -> ou <-)  est représentée par une étiquette c1/c2 d  sur l’arc reliant le sommet e1 au sommet e2.

 

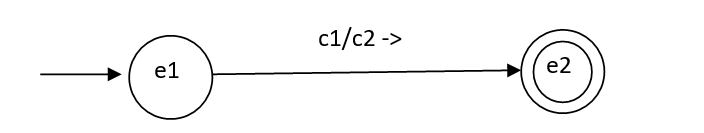
Une transition  F (e1, c3) = (e1, c3, d)  où e1 est dans E, c3  dans T et d est une direction ( -> ou <-)  est représentée par une étiquette c3 d  sur un arc de cercle reliant le sommet e1 à lui-même :

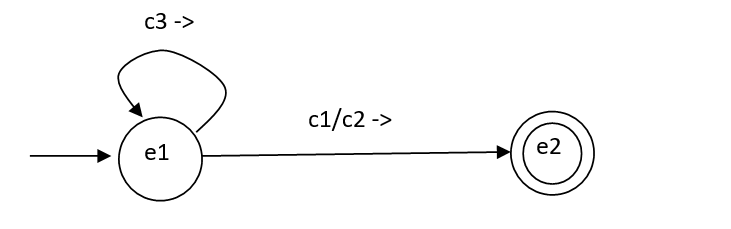
Une lorsqu’il existe plusieurs transitions du type précédent, on le note c3, c4, c5 d :

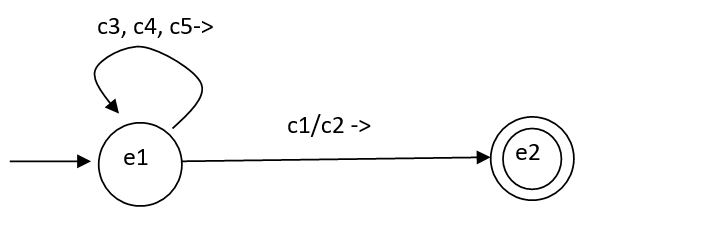
Le programme de l'exemple se décrit par le graphe suivant:

Créé avec HelpNDoc Personal Edition: Générateur d'aides CHM gratuit