Les Graphes: algorithmes
Objectifs
- Parcourir un graphe en profondeur d’abord, en largeur d’abord.
- Repérer la présence d’un cycle dans un graphe.
- Chercher un chemin dans un graphe.
Exercice 3
On considère un graphe orienté:
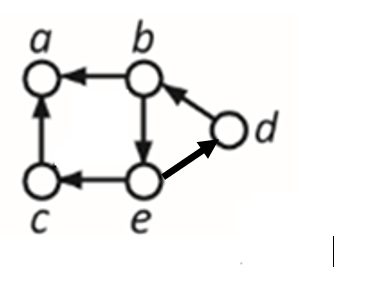
3.1 Donner les chemins de d vers a. Existe-t-il un chemin de a vers d ?
3.2 ce graphe est-il connexe ?
Exercice 4:
Vous disposez de la classe Graphe ci-dessous qui permet de créer des objets graphes:
class Graphe:
# méthode constructeur d'objet graphe
def __init__(self):
# création d’un dictionnaire vide adj qui représente le graphe pour l'objet self:
self.adj = {}
# méthode ajoute sommet s dans le dictionnaire adj
def ajouter_sommet(self, s):
# si le sommet n'est pas déjà dans le dictionnaire:
if s not in self.adj:
# création d'une clé s associée à un ensemble vide
self.adj[s] = set() # adj = { s:{} }
# méthode ajoute un arc orienté entre sommets s1 et s2
def ajouter_arc(self, s1, s2):
# création des deux sommets dans adj
self.ajouter_sommet(s1) # adj = { s1:{} }
self.ajouter_sommet(s2) # adj = { s1:{}, s2:{} }
self.adj[s1].add(s2) # adj = { s1:{s2}, s2:{} }
# méthode renvoie True si arc de s1 vers s2
def arc(self, s1, s2):
return s2 in self.adj[s1]
# méthode renvoie la liste des sommets
def sommets(self):
return list(self.adj)
# méthode renvoie l'ensemble des sommets voisins de s
def voisins(self, s):
return self.adj[s]
4.1 Coder le graphe de l'exercice 3 en utilisant des objets de cette classe
4.2 On considère ci-dessous la fonction parcours d'un graphe qui prend 3 paramètres un objet de la classe Graphe g, un objet set vus et un sommet s, utiliser cette fonction pour déterminer s'il existe un chemin entre deux sommets quelconques du graphe de l'exercice 3.
def parcours(g, vus, s):
"""parcours en profondeur du graphe g depuis le sommet s, renseigne un ensemble vus"""
if s not in vus:
vus.add(s) # sommet marqué
# pour chaque sommet v voisin de s dans g
for v in g.voisins(s):
parcours(g, vus, v)
4.3 Coder une fonction detecte_cycle qui prend en paramètre un objet de la classe Graphe g et un sommet s, la fonction doit renvoyer True si on rencontre un cycle en parcourant le graphe depuis un sommet quelconque s, la fonction doit renvoyer False si aucun cycle n’apparaît en partant de s. Voir un exemple de code en cliquant ici
Exercice 5: parcours en largeur d'un graphe
On considère le graphe ci-dessous:
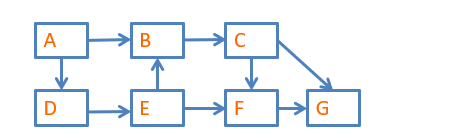
5.1 Coder le graphe
5.2 On cherche à définir le dictionnaire distances qui contient la distance minimale entre un des sommets et tous les autres. Définir manuellement ce dictionnaire pour le sommet B
5.3 Utiliser le code de la fonction parcours_largeur ci-dessous pour obtenir le dictionnaire distances pour le sommet A, pour voir le principe de fonctionnement du code de la fonction parcours cliquer-ici
def parcours_largeur(g, source):
"""parcours en largeur depuis le sommet source"""
dist = {source: 0} # un dictionnaire
courant = { source } # un ensemble
suivant = set() # un ensemble vide
while len(courant) > 0:
s = courant.pop()
for v in g.voisins(s):
if v not in dist:
suivant.add(v)
dist[v] = dist[s] + 1
if len(courant) == 0:
courant, suivant = suivant, set()
return dist
Exercice 6: l'algorithme de Dijsktra (hors programme de terminale, pour les très costauds)
Recherche du chemin le plus court entre deux sommets d'un graphe avec arcs pondérés
Regarder le diaporama sur le principe de l'algorithme de Dijsktra en cliquant ici:
On vous donne une version python de cet algorithme dans le fichier disjkstra.py pour un graphe de sommets étiquetés A jusqu'à I
Représenter le graphe en vous aidant de la matrice de pondération des arcs.
Vérifier votre représentation en demandant au programme de calculer le plus court chemin entre A et I
Modifier le programme pour afficher les sommets rencontrés dans ce chemin le plus court
Créé avec HelpNDoc Personal Edition: Créer des livres électroniques EPub facilement