La mise au point des programmes
Partie 1: préconditions-postconditions-exceptions
Exercice 1
On donne ici le code d'une fonction qui vérifie que les nombres d'un tableau t passé en argument à la fonction sont classées par ordre croissant:
def est_croissant(t:list) -> bool:
i=len(t) -1
while i >= 0:
if t[i] <= t[i+1]:
return True
else:
return False
i-= 1
a. Écrire les postconditions suivantes, en déduire si la fonction est conforme à ce que l'on attend d'elle:
t1 = [ 1, 2, 3, 4, 5, 6 ] ici la fonction doit renvoyer True
t2 = [ 1, 3, 2, 4, 5, 6 ] ici la fonction doit renvoyer False
t3 = [ ] ici la fonction doit renvoyer True
b. Pour trouver la cause du bug, vous allez utiliser le debugger de VS-Code, regarder la vidéo en cliquant ici
Après avoir déboguer la fonction, vérifier à nouveau les postconditions.
c.Remplacer la boucle while par une boucle for qui parcourt la liste en commençant par le dernier élément ( analyse du dernier élément vers le premier)
d. Écrire la précondition qui permettrait d’arrêter l'exécution de la fonction si on soumet le tableau
[1, 2, 3, 'B', 5, 6] en argument à la fonction.
Exercice 2
a. Proposer le code d'un programme qui demande n nombres entiers naturels à l'utilisateur du programme et les stockent dans un tableau t2, la valeur de n est choisie par l'utilisateur du programme durant l'exécution du code (voir un exemple rendu ci-dessous):

b. Écrire une gestion d'exception qui permettrait d’afficher le message "vous devez saisir un nombre entier naturel pour n" si l'utilisateur ne saisit pas un nombre entier pour n:

c. Ajouter une programmation défensive qui refuse la saisie si cette dernière n'est pas un nombre entier naturel, le programme ne doit pas s'interrompre ( exemple de rendu):

Exercice 3
On cherche maintenant à générer aléatoirement n nombres dans un tableau t3
a. Compléter la définition de la fonction tableau_croissant(n) qui renvoie un tableau trié par ordre croissant de n nombres générés aléatoirement. La définition de la fonction ne doit pas utiliser la méthode sort() pour triere
from random import randint
def tableau_croissant(n:int) -> list:
""" fonction qui génère et renvoie un tableau de n nombres aléatoires"""
t3 = [0] * n
return t3
# utilisation pour n=10 éléments
tableau_généré = tableau_croissant(10)
b.Expliquer la ligne t3 = [0] * n
Partie 2: Module et package
Exercice 1
a. Effectuer les actions suivantes:
- Créer un dossier appelé mon_dossier_travail
- Créer un package appelé mon_package dans le dossier mon_dossier_travail
- Ajouter un fichier __init__.py dans le package mon_package
- Ajouter un module appelé mon_module_1 dans le package mon_package
- Ajouter la fonction affichage ci-dessous dans le module mon_module_1
def affiche():
print("message depuis le module 1")
- Ajouter un module appelé mon_module_2 dans le package mon_package
- Ajouter la fonction affichage ci-dessous dans mon_module_2
def affiche():
print("message depuis le module 2")
- Ajouter un module appelé mon_module_principal dans le dossier mon_dossier_travail et en dehors du package.
b. Ajouter le code ci_dessous dans le module mon_module_principal :
import mon_package
from mon_package.mon_module_2 import *
from mon_package.mon_module_1 import *
affiche()
- tester le code et expliquer le résultat de l'affichage
c. Modifier le code précédent pour que ce soit la fonction affiche du module 2 qui soit utilisée
Partie 3: Interfaces
Exercice 1
a. Ajouter dans votre module mon_module_principal le code ci_dessous de deux fonctions qui détectent la présence de doublons dans un tableau :
def presence_doublon(t:list)-> bool:
s={}
for data in t:
if data in s.keys():
return True
else:
s[data] = 1
return False
def presence_doublon_2(t:list)-> bool:
s=[]
for data in t:
if data in s:
return True
else:
s.append(data)
return False
- tester les deux fonctions en passant en paramètre les tableaux ci-dessous :
tab1 = [1,2,3,2,4]
tab2 = [1,2,3,4,5]
- conclure sur la correction de ces deux fonctions ( correction = fonctionnement correct)
b. Vous pouvez voir que le code des deux fonctions n'a pas de documentation. Ajouter aux fonctions:
- une documentation,
- le type de données attendu pour t,
- le type de la valeur de retour.
c. Les parties rouges de chaque fonction ci-dessus sont liées à l'implémentation choisie pour le conteneur s. On désire remplacer ces parties par le code en vert ci-dessous qui encapsule cette implémentation:
def presence_doublon(t:list)-> bool:
s = creer_conteneur()
for data in t:
if est_present(data, s):
return True
else:
ajouter(data,s)
return False
- Ecrire l'interface qui présente les trois fonctions sur votre compte rendu
- Proposer une implémentation des deux fonctions est_present(data,s) et ajouter(data,s) qui permette de manipuler indifféremment une structure s de type dictionnaire ou liste, tout autre structure générerait un exception de type TypeError:
liste = [ 1,2,3]
dico = [ 1:True, 2:True, 3:True ]
print( contient(2,liste) ) # ici s = [ 1,2,3], affiche True parce que 2 est une clé de s
print (contient(4,dico) ) # ici s = [ 1:True, 2:True, 3:True ], affiche False parce que 4 n’est pas une clé de dico
liste = [1,2,3]
ajoute(4,liste) # s = liste et contiendra [1,2,3,4]
dico = { 1:True }
ajoute(2,dico) # s = dico et contiendra {1:True , 2: True}
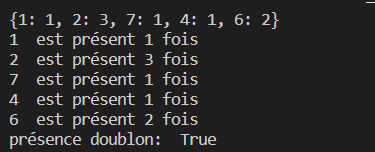
d. Ecrire la fonction compte_et_affiche_doublons(t) qui crée un dictionnaire avec comme clés les éléments du tableau t, la valeur de chaque clé étant le nombre d'occurrences des éléments, la fonction affichera le dictionnaire, le nombre d’occurrences de chaque élément et renverra True si t comporte des doublons ou False sinon.
Exemple de rendu pour le code d'utilisation suivant:

Créé avec HelpNDoc Personal Edition: Produire des livres Kindle gratuitement