Diviser pour régner
Partie 1: Révision de première sur la recherche dichotomique et le tri
Question 1.1
On considère la liste L = [ 1,3,2,4,7,6,5,8,9,12]
Écrire une fonction appelée tri_selection (L:list) qui prend en paramètre la liste L et qui trie cette liste en place (modifie directement la liste et non une copie ) en utilisant la méthode de tri vue en première appelée "tri-sélection".
Quelle est la complexité en temps de cette méthode de tri ? Justifier cette complexité.
Question 1.2
Écrire une fonction appelée verifie(L:list)-> bool qui prend en argument une liste L , vérifie qu'elle contient bien des nombres et renvoie True si la liste est triée. Pour la vérification du type de données de L voir le chapitre "Ressources".
Question 1.3
On veut maintenant retrouver rapidement si un nombre b est présent dans une liste triée L.
Écrire une fonction itérative appelée recherche_dichotomique (b:int, L:list)-> int qui prend en paramètres le nombre b recherché et la liste triée L. La fonction renverra la position de b dans la liste L si le nombre est présent ou -1 dans le cas contraire.
La fonction devra implémenter une programmation défensive ( voir le chapitre "Ressources" ), c'est à dire:
- une gestion d'exception globale avec try-except
- la vérification du type de donnée de b avec isinstance( ...)
- la vérification du type de donnée de L avec isinstance( ...)
- la vérification que la liste est triée et contient bien des nombres.
Tester le code pour la recherche de b=2
Tester le code pour la recherche de b=10
Question 1.4
Écrire une fonction recursive appelée recherche_dichotomique ( b:int, L:list, min:int = 0, max:int=len(L)-1 ) -> int
La fonction prend en paramètres le nombre b, une liste triée L, min est la valeur de l'indice du premier élément de la liste au départ fixé à 0 et max est la valeur du dernier élément de la liste au départ fixé à len(L)-1. La fonction devra renvoyer la position de b dans la liste L si le nombre est présent ou -1 dans le cas contraire.
Vous mettrez en place une programmation défensive en dehors de la fonction (avant son appel) , par exemple l'appel de la fonction ne pourra pas se faire si L est vide
Tester le code pour la recherche de b=2
Tester le code pour la recherche de b=10
Partie 2: recherche du minimum d'une liste avec la méthode diviser pour régner
On considère la liste L = [ 23,12,15,4,45,6,8,7,56,3,12,46]
On va utiliser une méthode diviser pour régner afin de déterminer récursivement la valeur minimum de cette liste:
- On divise la liste en deux sous liste
- On calcule récursivement le minimum des deux sous listes (on arrête la récursivité lorsque les listes n'ont plus qu'un seul élément).
- On renvoie le plus petit des deux éléments précédents.
Voici le pseudo-code:
def minimum( L,d,f):
''' L est une liste, d est l'indice du début de la recherche, f est l'indice de la fin de la recherche '''
si d==f:
retourner L[d]
sinon:
m = (d + f) //2
x = minimum( L, d, m)
y = minimum ( L, m+1, f)
si x < y:
retourner x
sinon:
retourner y
Question 2.1
Coder la fonction minimum en python et la tester sur la liste L précédente.
Partie 3: Tri-fusion
On vous propose ici de trier une liste par tri-fusion
La méthode sera la suivante:
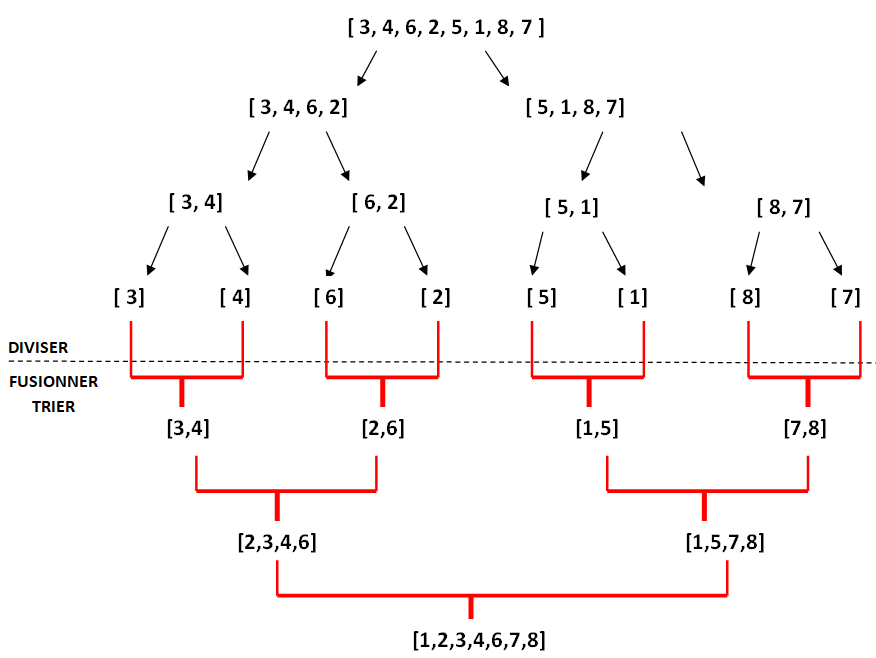
On divise d'abord la liste en deux puis on divise chaque sous liste récursivement jusqu'à l’obtention de sous listes d'un seul élément.
On fusionne ensuite deux à deux les éléments, en les triant par ordre croissant.
Le schéma ci-dessous illustre le principe:
Question 3.1
Coder en python la fonction fusion(L1, L2) qui fusionne dans l'ordre croissant deux listes L1 et L2 préalablement triées
.
Question 3.2
Voici le pseudo code de la fonction récursive tri_fusion qui divise + trie + fusionne ( elle utilise votre fonction fusion) .
def tri_fusion( L):
nbre = nombre d'éléments de L
si nbre <= 1:
retourner L
sinon:
L1 = []
L2 = []
pour tout x dans la plage [ 0, nbre//2[:
L1 = ajouter L[x]
pour tout x dans la plage [nbre//2, nbre[:
L2 = ajouter L[x]
retourner( fusion( tri_fusion(L1), tri_fusion(L2)))
Coder en python la fonction tri_fusion(L) puis tester votre code sur la liste L= [ 3, 4, 6, 2, 5, 1, 8, 7 ]
Partie 4: diviser pour régner ( rotation d'une photo)
Dans cette partie vous allez utiliser une méthode "diviser pour régner" afin de retourner une image.
Notions préalables:
Vous allez utiliser la bibliothèque PIL de python qui permet de manipuler les pixels d'une image, voici un exemple de code qui permet de créer un objet image appelé im à partir du fichier d'une image "carre.bmp", le code crée ensuite un objet appelé px qui représente le tableau des pixels de l'image ( lire ce code ne pas l'implémenter, vous n'avez pas le fichier carre.bmp )
# chargement de la classe Image du module PIL
from PIL import Image
# création de l'objet im qui représente l'image en mémoire du fichier "carre.bmp"
im = Image.open("carre.bmp")
# initialisation de deux variables qui contiendront les dimensions en pixels de l'image
largeur, hauteur = im.size
# initialisation de la variable px qui sera un tableau de pixels de l'image
px = im.load()
On considère une image de 4 pixels par 4 pixels, vous pouvez voir ci-dessous comment sont repérés les coordonnées x, y de chacun des pixels :

A savoir: il est plus simple de manipuler des images carrées ( nombre de lignes de pixels = nombre de colonnes de pixels) dont le nombre total de pixels est une puissance de 2, ci-dessus c'est le cas avec 16 pixels = 24
Pour obtenir cette image appelée carre.bmp, on pourrait utiliser le code python suivant:
# Ajout de fonctionnalités de la bibliothèque PIL (traitement d'image en python)
from PIL import Image
# crée une image de 4 lignes et 4 colonnes de pixels en RGB ( red, green, blue)
img = Image.new("RGB",(4,4))
# pour chacune des 2 premières colonnes
for colonne in range(2):
# pour les deux premières lignes
for ligne in range(2):
# on colore le pixel en rouge
img.putpixel((colonne,ligne),(255,0,0))
# pour les deux dernières lignes
for ligne in range(2,4):
# on colore le pixel en vert
img.putpixel((colonne,ligne),(0,255,0))
# pour chacune des 2 dernières colonnes
for colonne in range(2,4):
# pour les deux premières lignes
for ligne in range(2):
# on colore le pixel en jaune
img.putpixel((colonne,ligne),(255,242,0))
# pour les deux dernières lignes
for ligne in range(2,4):
# on colore le pixel en bleu
img.putpixel((colonne,ligne),(0,0,255))
# sauvegarde de l'image en tant que fichier carre.bmp
img.save("carre.bmp")
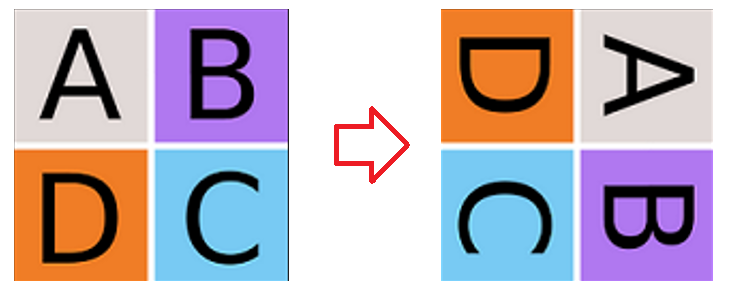
Maintenant vous allez implémenter la méthode diviser pour régner afin de pivoter l'image ci-dessous de 90° dans le sens horaire:
Méthode 1:
Le code se base:
L’instruction image.crop(zone) où zone est un quadruplet (g,h,d,b) renvoie une copie de la zone de l’image constituée des pixels (x,y)
pour x allant de g (« gauche ») à d (« droit ») et y de h (« haut ») à b (« bas »), l'instruction sert à découper l’image.
L’instruction image.paste(coord, im) colle l’image im dans image en mettant son coin en haut à gauche aux coordonnées coord = (x,y).
Elle nous sert à combiner les blocs.
- Télécharger l'image carre.png ( cliquer ici) et la copier dans le dossier du projet.
- Tester le code ci-dessous qui utilise ces deux instructions pour pivoter l'image:
from PIL import Image
# On crée une fonction appelée rotation
def rotation(image):
m, n = image.size
# si l'image est carrée et si la taille est une puissance de 2
if m == n and (n & (n - 1) == 0):
# si n = 1 on ne fait plus rien (un seul pixel)
if n > 1:
# on calcule le milieu
k = n // 2
# Division de l'image en 4 blocs
A = image.crop((0, 0, k, k))
B = image.crop((k, 0, n, k))
C = image.crop((k, k, n, n))
D = image.crop((0, k, k, n))
# Résoudre : rotation des blocs ( appel récursif)
rotation(A)
rotation(B)
rotation(C)
rotation(D)
# Combiner : permutation des blocs
image.paste(D, (0, 0))
image.paste(A, (k, 0))
image.paste(B, (k, k))
image.paste(C, (0, k))
return image
# Appel de la fonction et affichage
# chargement et affichage de l'image d'origine
monimage = Image.open("carre.png")
monimage.show()
# rotation et affichage de l'image obtenue
monimage2 = rotation(monimage)
monimage2.show()
Exercice 4.1
Pourquoi dit-on que la fonction rotation est récursive?
Exercice 4.2
On s'intéresse à la ligne de code ci-dessous que l'on trouve au début du code de la fonction rotation:
if m == n and (n & (n - 1) == 0):
4.2.1: on considère une image de 16 pixels: m = 4 (lignes de pixels) et n = 4 (colonnes de pixels)
Évaluer le résultat booléen (True ou False) du test: m == n dans ce cas.
Évaluer le résultat booléen (True ou False) du test : n & (n - 1) == 0 sachant que cette expression veut dire que le résultat du & "et logique" entre les bits des deux nombres numériques n = 4 ( en binaire 0100) et n -1 = 3 ( en binaire 0011) doit être égal à 0)
En déduire le résultat du test "if" en effectuant un "and" ( et logique ) entre les deux booléens obtenus précédemment.
4.2.2: On considère maintenant une image de 25 pixels: m = 5 (lignes de pixels) et n = 5 (colonnes de pixels)
Évaluer le résultat booléen (True ou False) du test: m == n dans ce cas.
Évaluer le résultat booléen (True ou False) du test : n & (n - 1) == 0
En déduire le résultat du test "if" en effectuant un "and" (et logique) entre les deux booléens obtenus précédemment.
4.2.3: sachant que le code ne peut s'exécuter correctement que si l'image est carrée et si le nombre de pixels est une puissance de 2, quelle partie du test if étudié précédemment permet d'évaluer que l'image est carrée et quelle partie du test permet d'évaluer que le nombre de pixels est une puissance de 2 ?
Exercice 4.3
Pour comprendre l'exécution du code de la fonction rotation, on vous demande de décrire le déroulement du code pour une image carre.png de taille = 4 pixels ce qui donnera m=2 et n=2 ( renvoyé par im.size au début de la fonction rotation)
Méthode 2:
On va maintenant utiliser un code qui permute les blocs avant de leur appliquer la rotation ( voir ci-dessous) . Cliquez-ici pour voir un gif animé de l'évolution de l'image durant l'exécution du code.

- Tester le code ci-dessous:
from PIL import Image
def permutation_blocs(image, zone):
g, h, d, b = zone
k = (d - g) // 2
x, y = g + k, h + k
for i in range(k):
for j in range(k):
pixelA = image.getpixel((g + i, h + j))
pixelB = image.getpixel((x + i, h + j))
pixelC = image.getpixel((x + i, y + j))
pixelD = image.getpixel((g + i, y + j))
image.putpixel((g + i, h + j), pixelD)
image.putpixel((x + i, h + j), pixelA)
image.putpixel((x + i, y + j), pixelB)
image.putpixel((g + i, y + j), pixelC)
def rotation (image, zone=None):
"""
Algorithme de rotation d'image par la méthode « diviser pour régner »
Entrées :
- image : image à tourner, au format PIL (ex.: image = Image.open("image.png"))
- zone : quadruplet (g,h,d,b) délimitant la zone de l'image à tourner
"""
if zone is None:
zone = (0, 0, image.width, image.height)
g, h, d, b = zone
if (d - g) == (b - h) and ((d - g) & (d - g - 1) == 0):
permutation_blocs(image, zone)
if d - g > 1:
x = (g + d) // 2
y = (h + b) // 2
rotation (image, (g, h, x, y))
rotation (image, (x, h, d, y))
rotation (image, (g, y, x, b))
rotation (image, (x, y, d, b))
return image
# Appel des fonctions et affichage
# chargement et affichage de l'image d'origine
monimage = Image.open("carre.png")
monimage.show()
# rotation et affichage de l'image obtenue
monimage2 = rotation(monimage)
monimage2.show()
Exercice 4.4
Outre la permutation avant la rotation, ce code présente une différence importante par rapport à la méthode 1, laquelle?
Aide: que change l'utilisation des fonctions getpixel() et putpixel() par rapport à l'utilisation des fonctions crop() et paste() de la méthode 1
Quel est le bénéfice par rapport à la méthode1?
Créé avec HelpNDoc Personal Edition: Produire des livres Kindle gratuitement