Partie 2 : Chiffrements asymétriques

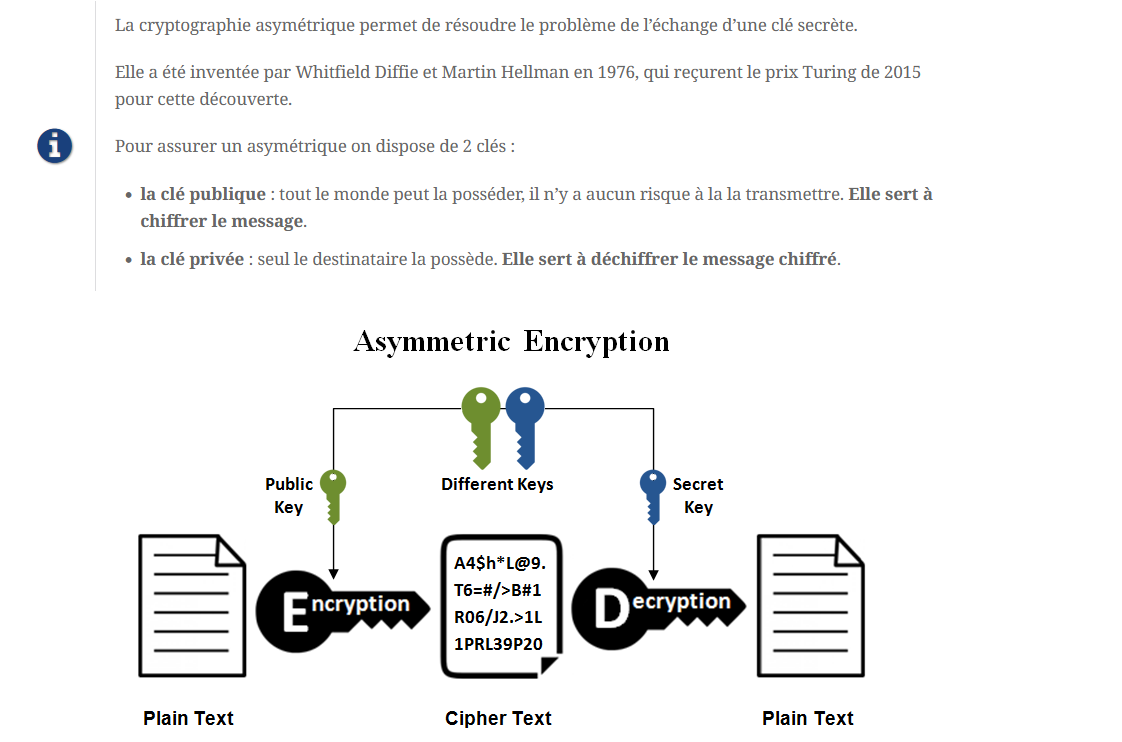
Pour que cela fonctionne, il faut que la paire clé publique/clé privée ait une propriété particulière.
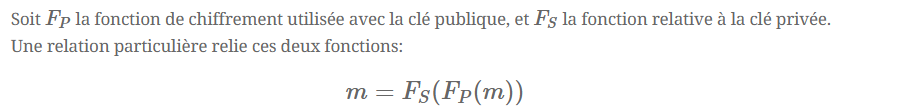

Un système qui satisfait ces deux critères est le système de chiffrement RSA utilisé pour échanger des données confidentielles sur Internet.
Cet algorithme fut inventé en 1977 par Ronald Rivest, Adi Shamir et Leonard Adleman (initiales RSA) breveté par le MIT en 1983. Le brevet a expiré le 21 septembre 2000 ce qui permet de l’utiliser librement depuis.
Exercice 4: le chiffrement RSA
Principe:

Exemple de calcul :
Pour que le code soit difficile à décrypter, il faut de très grands nombre premier ce qui ne sera pas le cas de l'exemple pour faciliter les calculs:

L’algorithme RSA de génération des clés nécessite le calcul du PGCD de deux nombres. Commençons par nous doter d’une fonction pgcd(n,m) qui retourne le plus grand diviseur commun de deux nombres entiers n et m.
4.1 Coder la fonction pgcd(n,m) qui retourne le plus grand diviseur commun de deux nombres entiers n et m.
Aide: écrire une fonction recursive pgcd(m,n)
Cas de base: si n=0 renvoyer m
Cas récursif: sinon renvoyer le calcul de pgcd avec n comme premier argument et le modulo de m par n (m%n) en second argument.
4.2 Compléter les parties pointillées de la fonction generate_keys(p,q) qui retourne une liste contenant une paire de clés à partir de deux nombres premiers p et q :
Pour p = 29 et q = 31 vous devez obtenir clé publique : (11, 899) et clé privée : (611, 899)
def generate_keys(p,q):
# calcul de n
n = .................
# calcul de phi(n)
phi = ...............
#calcul de e
e=2
while e <....... and pgcd(.....)!= .....:
e+=1
# calcul de d
d = 1
# tant que e*d-1 n'est pas multiple de phi
while ......:
d +=1
# retourne la clé publique et la clé privée (dans cet ordre !)
return [(e,n),(d,n)]
p = int(input("p = "))
q = int(input("q = "))
keys = generate_keys(p,q)
public_key = keys[0]
private_key = keys[1]
print("clé publique :", public_key)
print("clé privée : ", private_key)
4.3 Compléter les parties pointillées la fonction encrypt_rsa(public_key, plaintext) qui retourne le message en clair plaintext chiffré à l’aide de la clé public_key
def encrypt_rsa(public_key, plaintext):
#public_key est un tuple : (e,n)
e = .....
n = .....
# texte chiffré, ne contient rien au commencement
ciphertext = ....
# Pour chaque caractère dans le message en clair
for car in .....:
# on ajoute au message chiffré le caractère chiffré : C = M**e % n
# On travaille sur le code utf-8 (valeur numérique) du caractère avec chr() et ord()
ciphertext += ......
#retourne le message chiffré
return ciphertext
4.4 Coder la fonction decrypt_rsa(private_key, ciphertext)
Remarque : Aidez vous de la fonction précédente encrypt_rsa et de la définition du déchiffrement RSA : M = Cd % n
Attaque par brute force
Une attaque par brute force consiste à tester des clés de déchiffrement jusqu’à ce qu’on trouve la bonne, c’est à dire jusqu’à ce que le message à déchiffrer apparaisse en clair. Dans le cas de RSA, cette technique consiste à trouver le paramètre d de la clé privée connaissant le paramètre n. Le travail est simplifié si on connaît une partie du message à déchiffrer.
4.5 Tester la fonction brute_force(n, list_cipher_char, contain) qui retourne la clé privée de déchiffrement RSA connaissant le paramètre n qui est connue grace à la clé publique, un message chiffré à l’aide de la clé à casser et une partie du message d’origine en clair (connue ou supposée) contain.
Si au terme de 10000 tentatives la clé n’est pas trouvée, la fonction retourne False
Remarque : Alan Turing a utilisé cette technique qu’on appelle indice de coïncidence pour rechercher un motif connue dans les messages allemands cryptés avec Enigma

- Decrypter la clé de déchiffrement sachant que :
- clé publique : (1903, 2117)
- Le message en clair contient NSI
- message chiffré :
['0x812', '0x171', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x3e1', '0x156', '0xe9', '0x83', '0x6e7', '0x5cc', '0x370', '0x582', '0x171', '0x1fb', '0x6e7', '0x370', '0x78b', '0x6e7', '0x370', '0x3de', '0x6e7', '0x4a4', '0x4a4', '0x709', '0x771', '0x6e7', '0x17b', '0x370', '0x78b', '0x199', '0x6e7', '0x4a4', '0x3f7', '0x370', '0x49b', '0xe9', '0x6e7', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x709', '0x83', '0x6e7', '0x5cc', '0x370', '0x3de', '0x6e7', '0x3d5', '0x6e7', '0x1fb', '0x370', '0x2f', '0x370', '0x212', '0x171', '0x6e7', '0x3d5', '0x370', '0x83', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3de', '0x171', '0x4a4', '0x4a4', '0x171', '0x156', '0x3d5', '0x817', '0x5ca', '0x7ff', '0x197', '0x582', '0x171', '0x78b', '0x171', '0x3f7', '0x709', '0x3f7', '0x171', '0x156', '0x3d5', '0x370', '0x23d', '0x23d', '0x23d', '0x5ca', '0x4fb', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3e1', '0x1fb', '0x156', '0xcd', '0x6e7', '0x4a4', '0x4a4', '0x6e7', '0xe9', '0x1fb', '0x370', '0x3e3', '0x6e7', '0x370', '0x750', '0x812', '0x124']
Remarque : Le message chiffré est constitué des codes utf-8 de chaque caractère en hexadécimal car certains caractères ne sont pas imprimables.
Ce format oblige à changer le code de la fonction de déchiffrement decrypt_rsa dont la nouvelle version est donnée ci-dessous:
def decrypt_rsa(private_key, list_cipher_char):
d = private_key[0]
n = private_key[1]
plaintext = ""
for car in list_cipher_char:
plaintext += chr(int(car,16)**d % n)
return plaintext
def brute_force(n, list_cipher_char, contain):
plaintext = ""
d = 1
# tant que le motif recherché (contain) n'apparait pas dans le message déchiffré
while contain not in plaintext:
# limite à 10000 tentatives avant de retourner False
if d > 10000:
return False
d+=1
# on tente de déchiffrer la liste des caractères du message chiffré avec la clé à tester
plaintext = decrypt_rsa((d,n),list_cipher_char)
print(f"clé : {(d,n)} => '{plaintext}'")
# ça a marché ! on retourne la clé trouvée sous forme d'un tuple
return (d,n)
public_key = (1903, 2117)
message_chiffre_hex = ['0x812', '0x171', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x3e1', '0x156', '0xe9', '0x83', '0x6e7', '0x5cc', '0x370', '0x582', '0x171', '0x1fb', '0x6e7', '0x370', '0x78b', '0x6e7', '0x370', '0x3de', '0x6e7', '0x4a4', '0x4a4', '0x709', '0x771', '0x6e7', '0x17b', '0x370', '0x78b', '0x199', '0x6e7', '0x4a4', '0x3f7', '0x370', '0x49b', '0xe9', '0x6e7', '0x370', '0x83', '0x156', '0xe9', '0x4a4', '0x370', '0x709', '0x83', '0x6e7', '0x5cc', '0x370', '0x3de', '0x6e7', '0x3d5', '0x6e7', '0x1fb', '0x370', '0x2f', '0x370', '0x212', '0x171', '0x6e7', '0x3d5', '0x370', '0x83', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3de', '0x171', '0x4a4', '0x4a4', '0x171', '0x156', '0x3d5', '0x817', '0x5ca', '0x7ff', '0x197', '0x582', '0x171', '0x78b', '0x171', '0x3f7', '0x709', '0x3f7', '0x171', '0x156', '0x3d5', '0x370', '0x23d', '0x23d', '0x23d', '0x5ca', '0x4fb', '0x156', '0x3f7', '0x1fb', '0x6e7', '0x370', '0x3e1', '0x1fb', '0x156', '0xcd', '0x6e7', '0x4a4', '0x4a4', '0x6e7', '0xe9', '0x1fb', '0x370', '0x3e3', '0x6e7', '0x370', '0x750', '0x812', '0x124']
private_key = brute_force( public_key[1], message_chiffre_hex, 'NSI')
if private_key:
print(f"Clé cassée : {private_key}")
else:
print("Pas réussi à casser la clé")
Créé avec HelpNDoc Personal Edition: Générateur de documentations PDF gratuit