REPRESENTATION D'UN TEXTE EN MACHINE
Présentation
Les appareils numériques que vous utilisez tous les jours ( smartphones, tablettes, ordinateurs, etc...) "manipulent" des informations ( images, sons, textes) qui sont représentées dans l'appareil numérique par des nombres binaires ( des suites de 0 et de 1). Un texte est constitué de mots , un mot est lui même un ensemble de caractères.
Les nombres binaires utilisés pour représenter les mots des textes représentent le codage de chaque caractère des mots; le codage binaire de chaque caractère est défini dans des tables selon une norme qui précise le nombre et l'organisation des bits.
La norme ASCII
Cette norme de représentation des caractères avec un ordinateur ( voir fig 1 ci-dessous) a été la première norme imaginée, elle est destinée aux caractères de la langue Anglaise, c'est le codage utilisé par beaucoup logiciels Américains. Voici un extrait de la table ASCII, les explications sont données en dessous des tables.
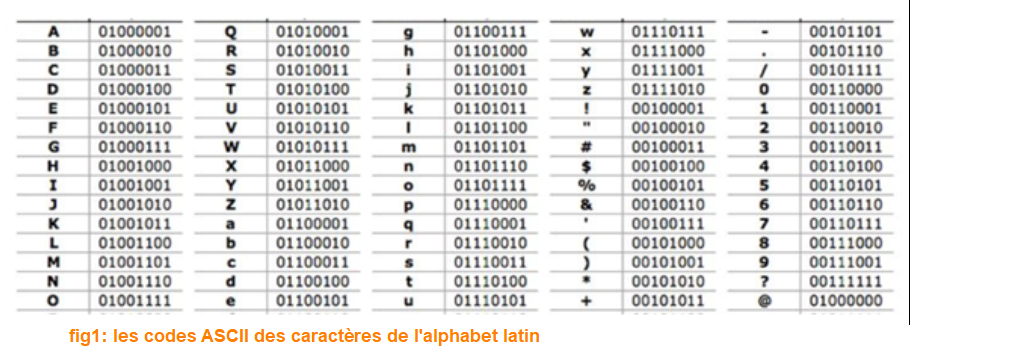
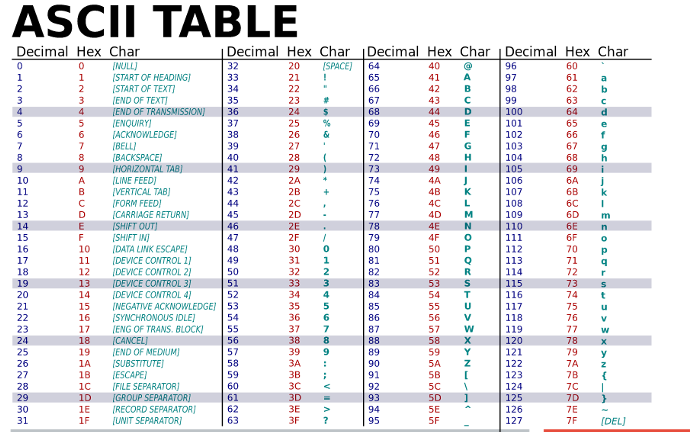
fig1 (partie droite)
La table ASCII peut être présentée de plusieurs façons, la table à gauche ci-dessus, vous donne le nombre binaire associé à chaque caractère, ce nombre est représenté sur un octet. La table de droite vous donne pour chaque caractère ( colonne Char) le nombre binaire converti en décimal et en Hexadécimal ( Hex).
Ainsi le caractère A est le nombre 0100 0001 en binaire, si on convertit ce nombre en décimal on obtient 65 et si on le convertit en hexadécimal 41.
Conclusion, en ASCII , le caractère A est codé par le nombre binaire 0100 001 (2) soit 65 (10) en décimal et 41 (16) en hexadécimal.
Un texte comme: "TATA YOYO" se code "0101 0100 0100 0001 0101 0100 0100 0001 0010 0000 01011001010011110101100101001111" en binaire; pour simplifier la lecture, les logiciels spécialisés affichent plutôt la valeur des caractères d'un texte codé en ASCII dans la version hexadécimale, ce qui donne pour "TATA YOYO" : "54 41 54 41 20 59 4F 59 4F"
Le caractère de valeur binaire 0010 0000 soit 20 en hexadécimal représente l'espace entre TATA et YOYO
- La norme ISO-8859-1 (appelée "ISO-latin1")
Cette norme a été créée par la suite, pour ajouter les caractères accentués des langues occidentales comme le Français ( é,è,ê, etc..), l'Allemand ( ü, ä, ö, ...) ou encore l'Espagnol ( ñ, ... ).
La table ISO-latin1 est compatible avec la table ASCII, les caractères de la table ISO-latin1 déjà présents dans la table ASCII gardent la même valeur binaire écrite sur 8 bits, ce qui donne toujours un nombre de décimale est entre 0 et 127 ; les caractères non ascii ajoutés par la norme ISO-8859-1 ont une valeur binaire écrite sur 8 bits qui correspond à une valeur décimale entre 160 et 255. La table ci-dessous vous donne la valeur hexadécimale de chaque caractère avec une table de la norme ISO-8859-1 :
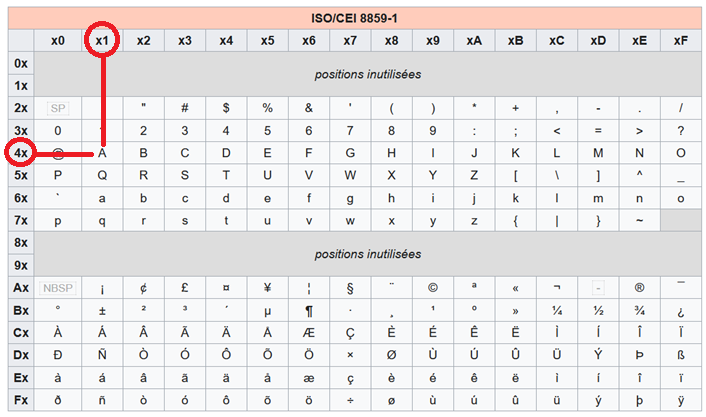
fig2: le caractère A vaut 4x et x1: on enlève les x et on fusionne les deux chiffres = 41 en hexadécimal (idem qu'en ASCII)
Plusieurs tables ( appelées pages de code) comme celle ISO-Latin1 ont été ajoutées, au fur et à mesure que l'informatique s'est développée, pour prendre en compte des nouvelles langues . Le problème des pages de code est qu’il n’était pas possible d’écrire des textes avec un mélange d’alphabets différents, ces derniers appartenant à des pages de code différentes.
- La norme ISO-10646
En 1989, l'Organisation internationale de normalisation définit la norme ISO-10646 qui décrit le jeu de caractères universel ( UCS pour Universal Character Set en Anglais), cette norme tente de donner à tous les caractères de toutes les écritures humaines connues une valeur numérique et un nom. Chaque caractère UCS possède donc un nom et un nombre associé appelé son point de code.
Les caractères UCS sont regroupés dans des tables, le caractère A est le caractère U+0041, le U+ précise que l'on a affaire à un caractère universel UCS et le 0041 est le point de code en représentation hexadécimale soit 0000 0000 0100 0001 en représentation binaire et 65 en décimal. Si on utilise directement le point de code du caractère A, on n'est pas compatible avec ASCII qui code le caractère A sur 8 bits (un octet).
Le Consortium UNICODE crée en 1991 différentes techniques de codages qui permettent d'utiliser plus ou moins de bits pour coder un caractère UCS. Ces techniques de codage sont appelées Formats de Transformation Universelle (UTF pour Universal Transformation Format en Anglais).
La transformation UTF-8 s'est imposée sur le WEB et dans beaucoup de logiciels qui manipulent des textes. UTF-8 est compatible avec ASCII, concrètement un site web qui a codé ses textes en ASCII s'affiche sans problème avec un navigateur qui utilise UTF-8.
Extraits de la table unicode:
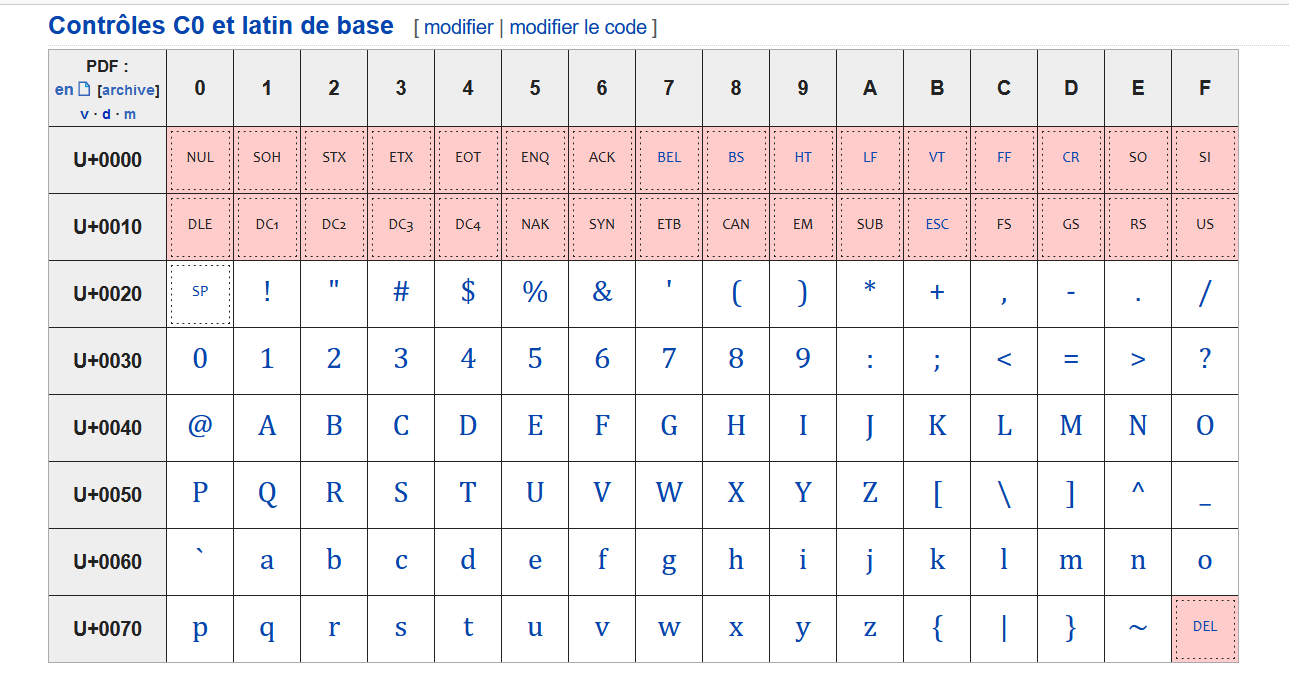
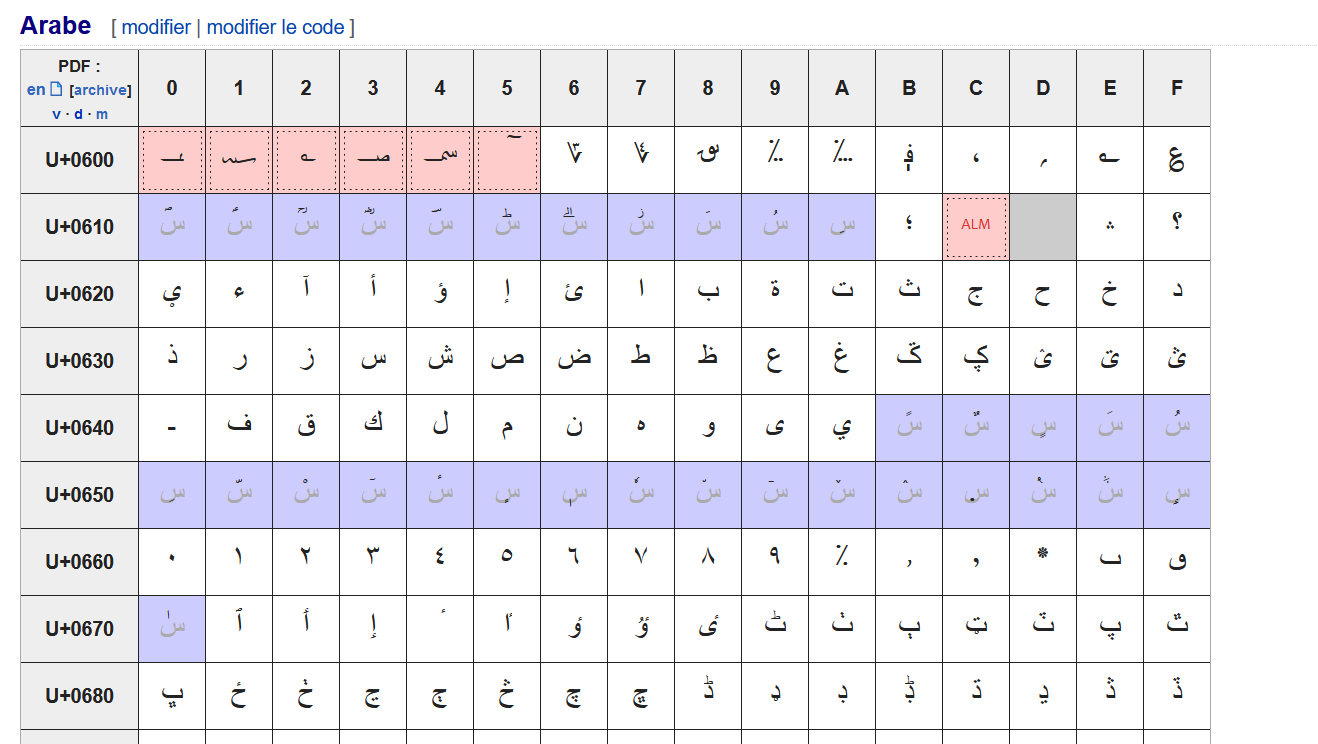
fig3
Les caractères UTF-8 sont codés sur 1, 2, 3 ou 4 octets. Voir les deux exemples ci-dessous:
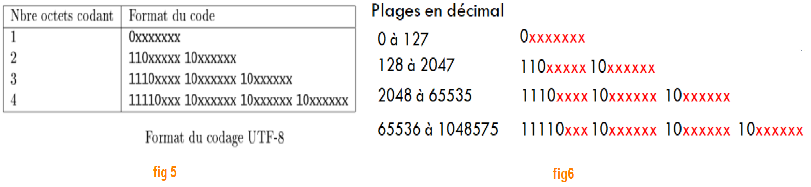
Le code UTF-8 est compatible avec ASCII, les caractères existants en ASCII sont codés sur 1 octet en UTF-8 ( la ligne 1 de la colonne Nbre octets codant du tableau fig 5 ). Un caractère existant en ASCII sera représenté en UTF-8 par un nombre dont le bit le plus à gauche est toujours égal à 0 ( comme montré à la ligne 1, colonne Format du code de fig 5), les autres bits du nombre dépendent du caractère, c'est pourquoi il y a des x dans la colonne Format du code.
Exemple1: le caractère A vaut 0100 0001 en ASCII, si on convertit ce nombre en décimal, on obtient 65. Les nombres dont la valeur décimale est entre 0 et 127 sont dans la table ASCII, ils ont un format de codage UTF-8: 0xxxxxxx comme le montre le tableau fig6.
En UTF8, A sera codé 0100 0001 comme en ASCII, le bit le plus à gauche est bien égal à 0.
Exemple2: le caractère é est le caractère U+00E9 de la table UCS, le point de code vaut 00E9 soit 0000 0000 1110 1001, si on convertit ce nombre en décimal on obtient 233. Les nombres dont la valeur décimale est entre 128 et 2047 sont codés sur deux octets en UTF-8, selon la forme: 110xxxxx 10xxxxxx, les x doivent être remplacés par les 11 bits les plus à droite du point de code du caractère codé:
ici é a le point de code: 0000 0000 1110 1001, on garde les 11 bits de droite ( ceux soulignés) que l'on met à la place des x pour obtenir le code UTF-8, le caractère é est donc codé en UTF-8 : 1100 0011 1010 1001 soit en hexadécimal c3 a9.
Il existe des tables utf-8, voici un extrait pour les caractères accentués, elle confirme notre codage:

fig7
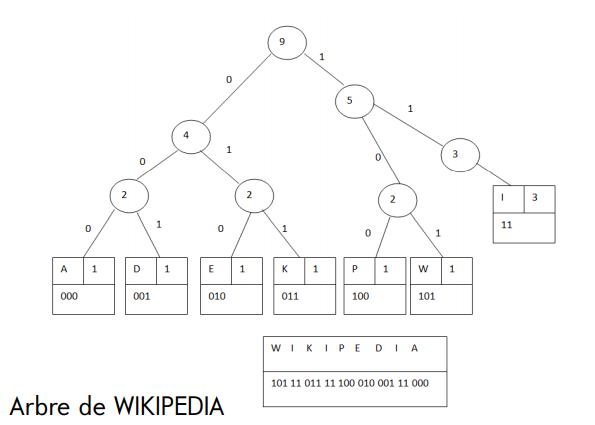
Codage de Huffman

Créé avec HelpNDoc Personal Edition: Création d'aide CHM, PDF, DOC et HTML d'une même source